POW 1, The More the Merriar
Overpopulation in Correlation to the quality of education in the US
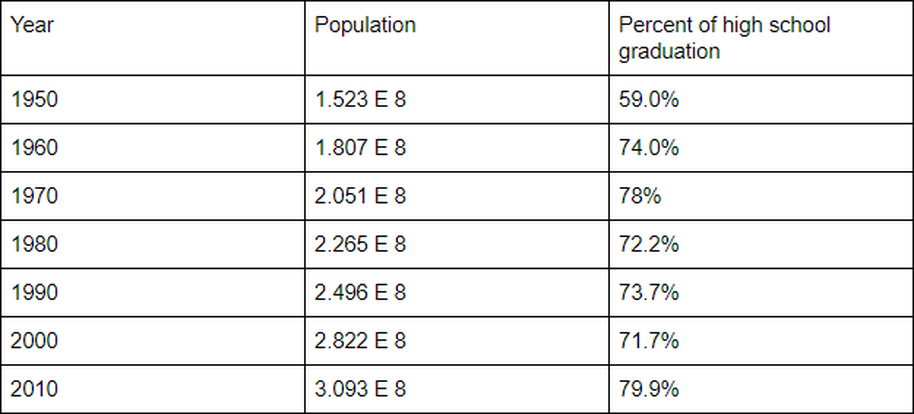
As population in the US grows I think about how overpopulation affect education in the US. With the population growing there will be progressively more students per school, which will in turn create more kids per class and less support for each individual student. I hypothesise that as population grows, kids will have less individual support resulting in less of the population finishing high school and graduating. I will test this by looking at population in comparison to percent of students finishing school and graduating ranging each decade from 1950 - 2010.
As you can see below, in sixty years this country's population has more than doubled, but if you look at the data you will see that a higher percentage of students have been graduating as time progresses. Although there is a lot of variance in rise and fall in high school graduation, overall the rates are going up. This disproves my hypothesis and sheds light on the fact that overpopulation does not have a vast effect on education in the US. I think that the data suggest that instead of making school have larger classes and a higher student per teacher ratio, that more school are being built and more teachers are being employed to compensate for the progressive rise in students.
Reflection: The More the Merrier POW involved us making up a problem about overpopulation and solving it, I chose to have mine be about how overpopulation affects the quality of education and thus affects the high school graduation rate. I am proud of this POW because I think the problem I came up with was creative and relevant to the question. I think I found a good testable question, as well as a good answer to that question. What made this POW enjoyable for me was the outlet for creativity in the question we are looking into.
As population in the US grows I think about how overpopulation affect education in the US. With the population growing there will be progressively more students per school, which will in turn create more kids per class and less support for each individual student. I hypothesise that as population grows, kids will have less individual support resulting in less of the population finishing high school and graduating. I will test this by looking at population in comparison to percent of students finishing school and graduating ranging each decade from 1950 - 2010.
As you can see below, in sixty years this country's population has more than doubled, but if you look at the data you will see that a higher percentage of students have been graduating as time progresses. Although there is a lot of variance in rise and fall in high school graduation, overall the rates are going up. This disproves my hypothesis and sheds light on the fact that overpopulation does not have a vast effect on education in the US. I think that the data suggest that instead of making school have larger classes and a higher student per teacher ratio, that more school are being built and more teachers are being employed to compensate for the progressive rise in students.
Reflection: The More the Merrier POW involved us making up a problem about overpopulation and solving it, I chose to have mine be about how overpopulation affects the quality of education and thus affects the high school graduation rate. I am proud of this POW because I think the problem I came up with was creative and relevant to the question. I think I found a good testable question, as well as a good answer to that question. What made this POW enjoyable for me was the outlet for creativity in the question we are looking into.
POW 2, Around King Arthur's Table
For this POW we were presented with the challenge of figuring out the pattern associated with a game made by King Camelot to make sure you always win. The game involves a random number of people sitting in a circle, the King walks up to the first member and says “You’re in.” and then walks up to the second member and say “You’re out.”. He repeats this process until everyone is either “In” or “Out”, the member than were told they were out left their chairs and the process repeats with the remaining members until there is only one person left, he is the winner. In this POW we had to figure out the pattern to decide by the number of people in the circle what spot to sit in, in order to win.
To figure out this problem I decided to first find general rules for who could be the winner. First I found that there would never be a winner sitting in an even number chair, because the first chair is always in therefore only odd numbered chairs are in. After that, I found all the possible values, which are just all odd numbers.. I made tables showing different amounts of guests and figured out who was going to win for each amount. I did this going from one guest to fourteen guests before I found a pattern. After I found a pattern I would take random amounts of guest and try and figure out who was going to be a winner using the pattern I found, and then compare that with a table.
My solution to this problem is that the winning number cycles through all odd number before going back down to one after a set amount of numbers gone through. The first cycle only includes one before restarting back to one, but after each cycle the number of odd numbers cycled through doubles. So for the second cycle there will be two odd numbers gone through, for the third cycle there will be four odd numbers gone through, and so on.
1st Cycle. 1
2nd Cycle, 1, 3
3rd Cycle. 1, 3, 5, 7
4th Cycle. 1, 3, 5, 7, 9, 11, 13, 15
5th Cycle. 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31
In this POW I learned how to analyze patterns in puzzles to figure out the math behind them and from there learn how to always win.
I think that I deserve a B on this POW. This is because although I didn’t get a complete answer I figured out the majority of the puzzle, I just couldn’t figure out how to apply the amount of people to where to sit by using an equation or rule, but by looking at a table where you have to count out the number of people in correlation to where to sit.
Reflection: The Around King Arthur's Table POW asked us to figure out the pattern behind a game that King Author created to figure out who wins a prize. The game involved the king going around in a circle saying every other person is out, he continues until everyone is out and only one person is left. I am proud of this POW because it challenged me to look at a pattern and take the long way to get a good result I am confident in. What made this problem enjoyable for me was when I finally found a good testable way of finding how to pattern continues.
To figure out this problem I decided to first find general rules for who could be the winner. First I found that there would never be a winner sitting in an even number chair, because the first chair is always in therefore only odd numbered chairs are in. After that, I found all the possible values, which are just all odd numbers.. I made tables showing different amounts of guests and figured out who was going to win for each amount. I did this going from one guest to fourteen guests before I found a pattern. After I found a pattern I would take random amounts of guest and try and figure out who was going to be a winner using the pattern I found, and then compare that with a table.
My solution to this problem is that the winning number cycles through all odd number before going back down to one after a set amount of numbers gone through. The first cycle only includes one before restarting back to one, but after each cycle the number of odd numbers cycled through doubles. So for the second cycle there will be two odd numbers gone through, for the third cycle there will be four odd numbers gone through, and so on.
1st Cycle. 1
2nd Cycle, 1, 3
3rd Cycle. 1, 3, 5, 7
4th Cycle. 1, 3, 5, 7, 9, 11, 13, 15
5th Cycle. 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31
In this POW I learned how to analyze patterns in puzzles to figure out the math behind them and from there learn how to always win.
I think that I deserve a B on this POW. This is because although I didn’t get a complete answer I figured out the majority of the puzzle, I just couldn’t figure out how to apply the amount of people to where to sit by using an equation or rule, but by looking at a table where you have to count out the number of people in correlation to where to sit.
Reflection: The Around King Arthur's Table POW asked us to figure out the pattern behind a game that King Author created to figure out who wins a prize. The game involved the king going around in a circle saying every other person is out, he continues until everyone is out and only one person is left. I am proud of this POW because it challenged me to look at a pattern and take the long way to get a good result I am confident in. What made this problem enjoyable for me was when I finally found a good testable way of finding how to pattern continues.
Semester Reflection
I liked this semester and it challenged me to recover some of my old math skills as well as learn new topics. I think that this semester I succeeded in my goals of learning. I was able to recover all of my algebra and geometry concepts as well as have a good handle on every concept we are learning in class.This semester I think that I realized that I should try and not wait until the last minute and instead I should work through my worksheets and problems over a period of days that gives me a completed product before the due date. I think that next semester I am going to try and procrastinate even less. I think that thi semester I have stopped for the most part, but I could still work harder to reduce my procrastination and have a better less stressful semester.
